全結合層

全結合層とは、DeepLearningで扱う関数の中で最も基本的なもの、もしくは概念といえます。
全結合層は以下のような関数で表せます。

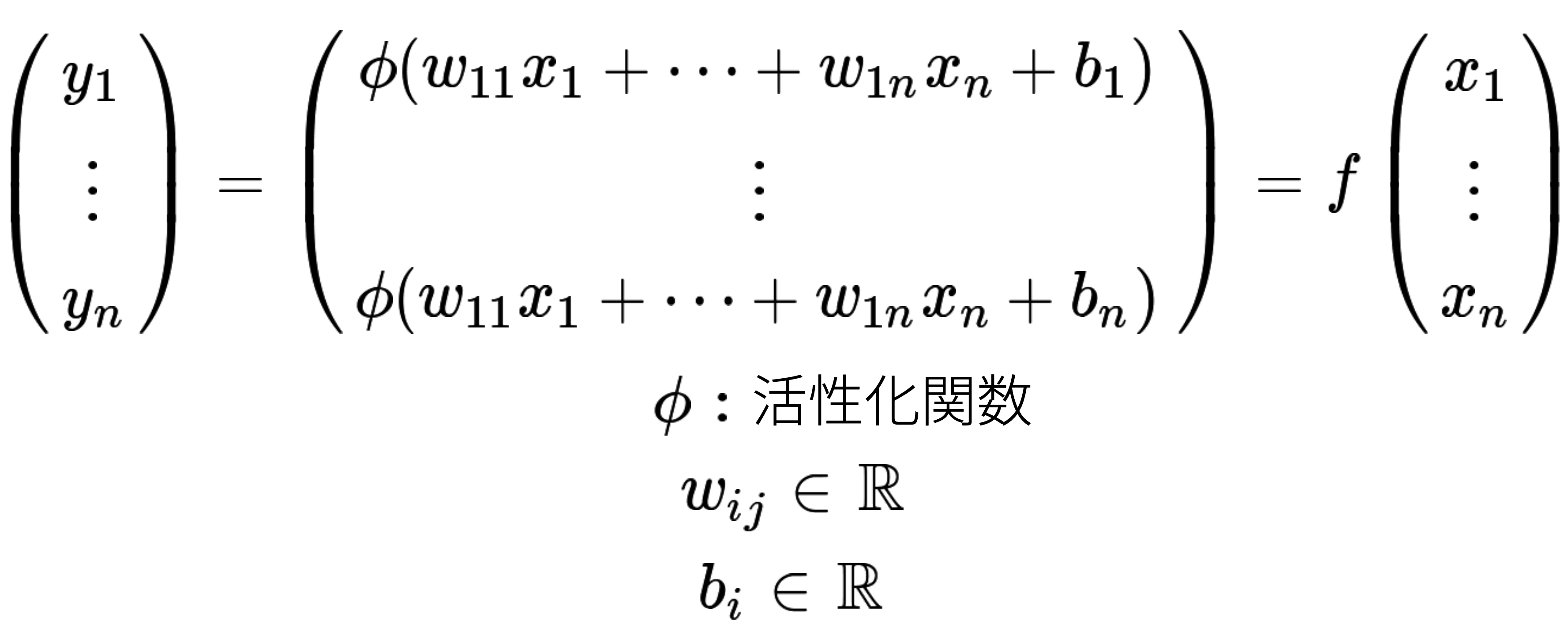
$$ \begin{pmatrix} y_1 \\ \vdots \\ y_n \\ \end{pmatrix} = \begin{pmatrix} \phi(w_{11}x_1 + \cdots + w_{1n}x_n + b_1) \\ \vdots \\ \phi(w_{11}x_1 + \cdots + w_{1n}x_n + b_n) \\ \end{pmatrix} = f \begin{pmatrix} x_1 \\ \vdots \\ x_n \\ \end{pmatrix} \\ \phi:\text{活性化関数} \\ w_{ij} \in \mathbb{R} \\ b_{i} \in \mathbb{R} \\ $$

大量の入力ベクトルデータ $(x_i)_{i=1...n}$ と出力ベクトルデータ $(y_i)_{i=1...n}$ が与えられ、$\sum_{i=1}^n ((y_i) - f(x_i))^2$ が最小の値になるように $w_{ij}, b_i$ を調整します。

実際にはこれだけだと関数として十分な表現力が得られず、精度の高い関数にはならないため、これらを合成して表現力を上げ、精度を高めます。

$$ \begin{pmatrix} y_1 \\ \vdots \\ y_n \\ \end{pmatrix} = f_k \begin{pmatrix} \cdots f_2 \begin{pmatrix} f_1 \begin{pmatrix} x_1 \\ \vdots \\ x_n \\ \end{pmatrix} \end{pmatrix} \cdots \end{pmatrix} \\ $$ この関数を模式図で表現すると $$ \begin{xy} \xymatrix { x_1 \ar[r]^{w_{11}^{(1)}} \ar[rd] \ar[rdd] \ar[rddd] \ar[rdddd] & b_1^{(1)} \ar[r]^{w_{11}^{(2)}} \ar[rd] \ar[rdd] \ar[rddd] \ar[rdddd] & b_1^{(2)} & \cdots & b_1^{(k)} \ar[r] & y_1 & &\\ x_2 \ar[ru] \ar[r] \ar[rd] \ar[rdd] \ar[rddd] & b_2^{(1)} \ar[ru] \ar[r] \ar[rd] \ar[rdd] \ar[rddd] & b_2^{(2)} & \cdots & b_2^{(k)} \ar[r] & y_2 & &\\ x_{i} \ar[ruu] \ar[ru] \ar[r] \ar[rd] \ar[rdd] & b_3^{(1)} \ar[ruu] \ar[ru] \ar[r] \ar[rd] \ar[rdd] & b_3^{(2)} & \cdots & b_i^{(k)} \ar[r] & y_i & \\ x_{n-1} \ar[ruuu] \ar[ruu] \ar[ru] \ar[r] \ar[rd] & b_{n-1}^{(1)} \ar[ruuu] \ar[ruu] \ar[ru] \ar[r] \ar[rd] & b_{n-1}^{(2)} & \cdots & b_{n-1}^{(k)} \ar[r] & y_{n-1} &\\ x_n \ar[ruuuu] \ar[ruuu] \ar[ruu] \ar[ru] \ar[r]^{w_{nn}^{(1)}} & b_{n}^{(1)} \ar[ruuuu] \ar[ruuu] \ar[ruu] \ar[ru] \ar[r]^{w_{nn}^{(2)}} & b_{n}^{(2)} & \cdots & b_n^{(k)} \ar[r] & y_n &\\ } \end{xy} $$

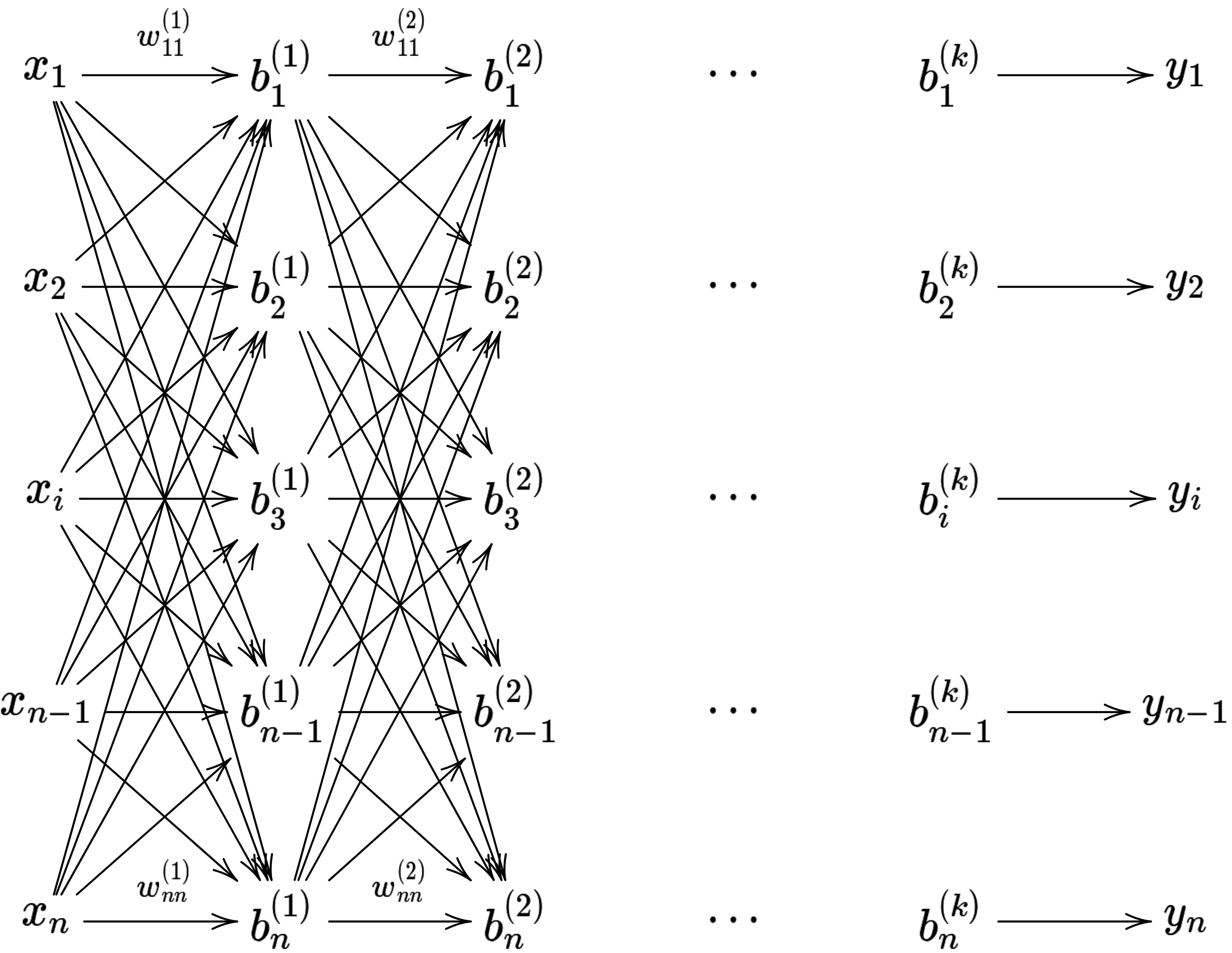
となり、これがニューラルネットワーク関数、およびディープラーニングと言われる所以となっています。

上記の例では、わかりやすくするために、入力層 $(x_i)$ , 中間層 $(b_i)$ , 出力層 $(y_i)$ を全て n 次元のベクトルとしましたが、これらは一致している必要性はありません。

扱いたいデータによりますが、通常、入力層は数千〜数百万になることはざらであり、中間層はパラメタを削減するために数百というオーダーにするケースが多いように思います。出力層も入力層同様、どのようなモデルを扱うかによりますが、数十から数万というようなオーダーになります。